Layer by Layer: Uncovering Where Multi-Task Learning Happens in Instruction-Tuned Large Language Models

Introduction

Instruction Tuning involves fine-tuning a language model on a collection of instruction-formatted multi-task datasets, with the goal of enabling the language model to generalize to unseen tasks. This paper investigates where and to what extent task-specific information is already encoded in the pre-trained language model and how instruction tuning affects the internal representations of these tasks in the model. Specifically, the authors investigate the following three research questions:

Research Questions

1. To what extent are different NLP tasks already encoded in pre-trained LMs?
2. How does instruction tuning modify the representational landscape of LMs?
3. Do the representational effects of instruction tuning generalize to unseen tasks?

Methodology

Standard probing methods involve building a model to perform a downstream task based on intermediate representations, with the goal of quantifying encoded information in them. But these methods can be limited because they rely on different metrics to evaluate performance across various tasks, making it challenging to directly compare the amount of information stored about various tasks as diverse as sentiment analysis and translation.

So, the authors use a sub-population technique called MOSSA - Model-Oriented Sub-population and Spectral Analysis - which involves comparing representations from two models - a control model and an experimental model. The control model is trained on the data relevant to the sub-population of interest (e.g., a specific task) and can be thought of as specialized in it. The experimental model is identical to the control model but is also trained on additional data from different sources (e.g., multiple tasks). MOSSA analyzes the differences in representations of the control and experimental models in order to understand what information is captured when a subset of the data is used versus the whole dataset. Intuitively, a high similarity between the experimental and control models indicates that the experimental model stores task-specific information learned by the control model, which was finetuned solely on the data from that task. For computing the similarity between representations, the authors use Central Kernel Alignment (CKA) metric, which measures alignment between representations in a kernel space, providing robust measure of similarity that is insensitive to scaling and centering.

Formally, let \([T]\) be an index set of tasks, and let \(\mathbf{E}\) be the experimental model and \(\mathbf{C}_t\) be the control model for task \(t\in[T]\). Let us assume a set of inputs \(\mathcal{X}=\cup_{t=1}^{T}\mathcal{X}_t\), where each \(\mathcal{X}_t={x_{t,1}, \dots, x_{t,n}}\) represents a set of input instructions for task \(t\). We assume that all sets have the same size n for simplicity. For each \(t\in[T]\) and \(i\in[n]\), we apply the experimental model \(\mathbf{E}\) and the control model \(\mathbf{C}_t\) to the input instructions \(x_{t,i}\) to obtain two corresponding representations \(\mathbf{y}_{t,i}\in\mathbb{R}^{d_t}\) and \(\mathbf{z}_{t,i}\in\mathbb{R}^{d_t}\), respectively. Here, \(d\) is the dimension of the experimental model representations, and \(d_t\) is the dimension of the control model representations for task \(t\). To obtain the representations \(\mathbf{y}_{t,i}\) and \(\mathbf{z}_{t,i}\), the authors use the last token representation, as LMs are auto-regressive and the last token captures all input information. These representations can be extracted from any layers of the respective models. By stacking these vectors into two matrices for each task \(t\), the paired matrices \(\mathbf{Y}_t\in\mathbb{R}^{n\times d_t}\) and \(\mathbf{Z}_t\in\mathbb{R}^{n\times d_t}\) are obtained. The CKA between the representations of the experimental and control models for task \(t\) is then computed as follows:

• The kernel matrices \(K_{\mathbf{Y}_t}\in\mathbb{R}^{n\times n}\) and \(K_{\mathbf{Z}_t}\in\mathbb{R}^{n\times n}\) for the representations \(\mathbf{Y}_t\) and \(\mathbf{Z}_t\) are computed using the same kernel function (e.g., linear, Gaussian or polynomial)
• Kernel matrices are then centered by \(K_{\mathbf{Y}_t}=K_{\mathbf{Y}_t}-\frac{1}{n}\mathbf{1}K_{\mathbf{Y}_t}-\frac{1}{n}K_{\mathbf{Y}_t}\mathbf{1}+\frac{1}{n^2}\mathbf{1}K_{\mathbf{Y}_t}\mathbf{1}\) (similarly for \(K_{\mathbf{Z}_t}\) where \(\mathbf{1}\) is a matrix of ones)
• CKA is first computed as the Frobenius inner product of the centered Gram matrices: \(HSIC(K_{\mathbf{Y}_t}, K_{\mathbf{Z}_t})=Tr(K_{\mathbf{Y}_t}^TK_{\mathbf{Z}_t})\), where \(Tr\) denotes the trace of a matrix. CKA value is then normalized:

\[CKA(\mathbf{Y}_t, \mathbf{Z}_t)=\frac{HSIC(K_{\mathbf{Y}_t}, K_{\mathbf{Z}_t})}{\sqrt{HSIC(K_{\mathbf{Y}_t}, K_{\mathbf{Y}_t})HSIC(K_{\mathbf{Z}_t}, K_{\mathbf{Z}_t})}}\]

Experiments and Results

60 NLP tasks from FLAN 2021 dataset are considered for the analysis. They are organized into 12 task clusters, where datasets within a given cluster belong to the same task type. To enhance instruction diversity, 10 unique natural language instruction templates are used for each dataset. The authors use the Llama-2-SFT (7B) model as a case study. There are two types of models: the experimental model \(\mathbf{E}\), finetuned using all \(T\) available tasks, and the single-task model \(\mathbf{C}_t\) for \(t\in[T]\), fine-tuned only on the \(t\)-th task. In some experiments, \(\mathbf{E}\) can also be the pre-trained model.

Results

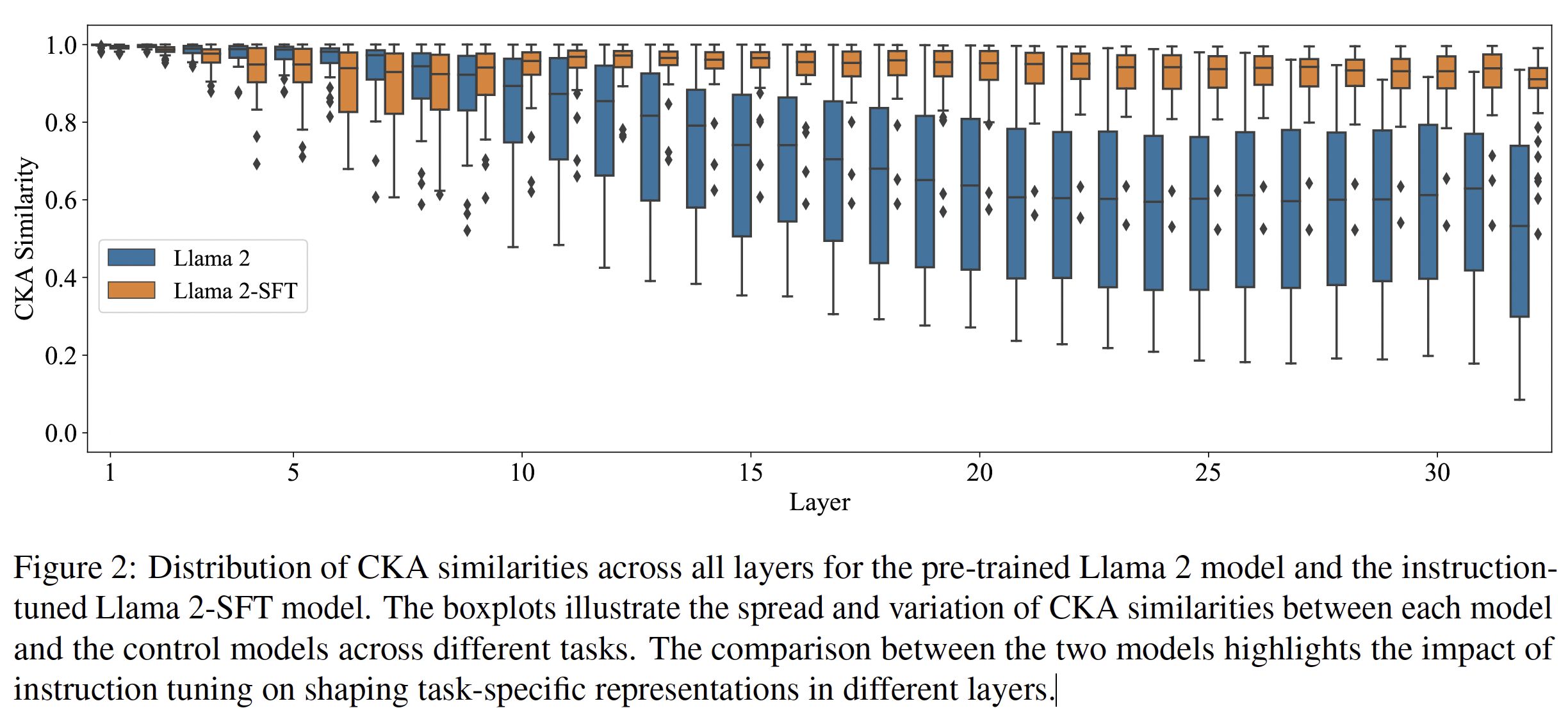
To what extent are different NLP tasks already encoded in pre-trained LMs?

Figure-2 shows the distribution of CKA similarities across all tasks and layers for the Llama-2 model. Llama-2 maintains high CKA similarities in earlier layers implying that representational changes in the earlier layers are minimal across tasks. However, in the middle and higher layers, there is a widespread variance in CKA across tasks i.e., some task representations in Llama-2 have high similarity with control model’s representations while others have low similarity. Since control models can be thought of as specialized in a particular task, this means that some tasks are better captured in Llama-2 model representations than others.

To get a finer understanding, the authors analyzed CKA results at the task cluster level, where each cluster consists of a group of similar tasks.

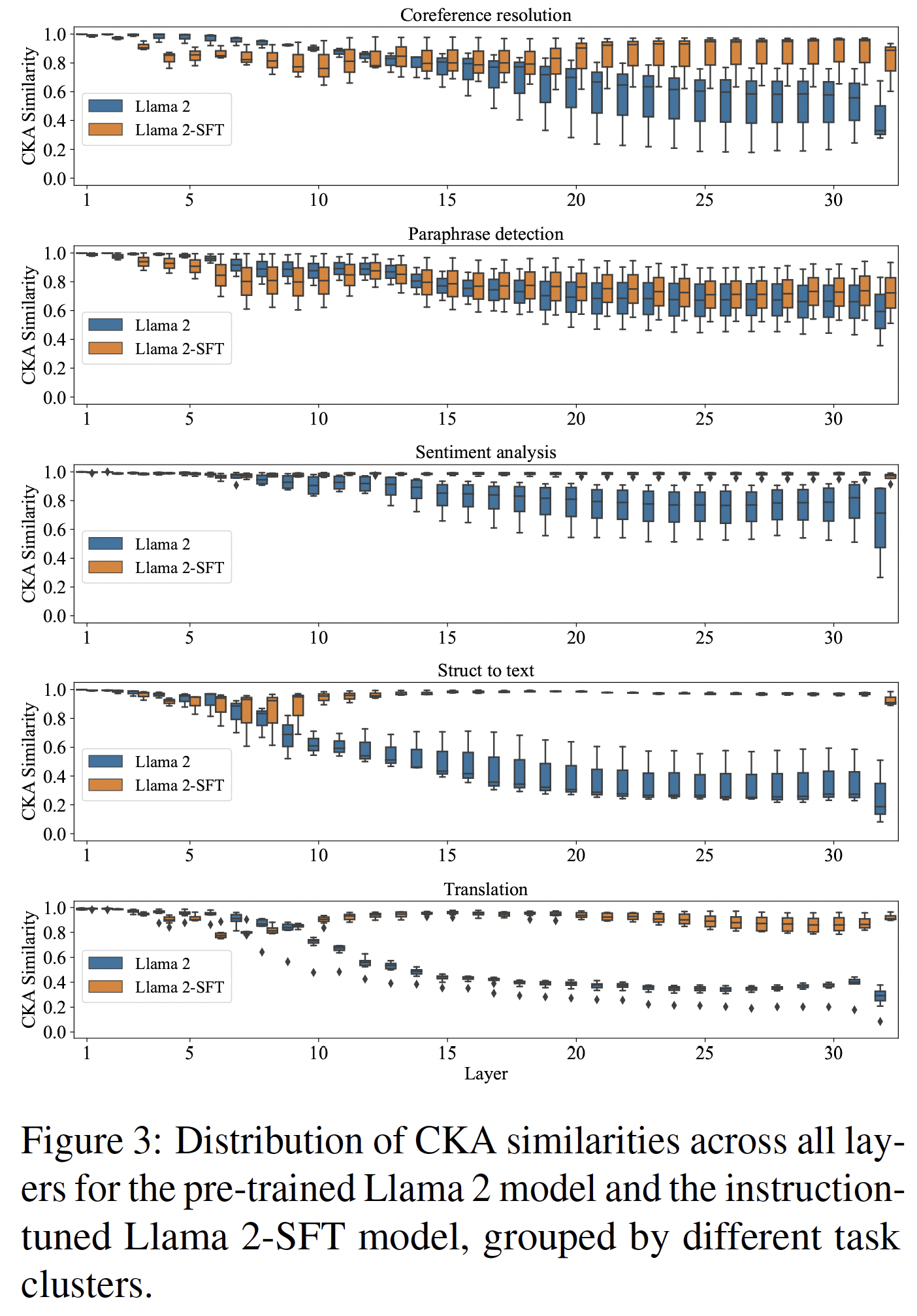
For clusters like closed-book QA, commonsense reasoning, paraphrase detection, and sentiment analysis, which heavily rely on general linguistic and semantic understanding, the CKA similarity for Llama-2 is high, indicating that pre-trained LMs already encode these tasks well in their representations. Conversely, for clusters like coreference resolution, reading comprehension, structured data to text generation, summarization, and translation, which require specialized, structured or domain-specific knowledge involving complex transformations or extended context management, the CKA simiarities are low, suggesting that next token prediction at pre-training is insufficient for encoding these tasks.

How does instruction tuning modify the representational landscape of LMs?

Mapping layers to their functionality

As illustrated in Figure-2, the CKA similarities between Llama-2-SFT and control models do not decrease as significantly as those for the pre-trained model across layers.

• In early layers (1 to 9), for many tasks, CKA scores are lower for Llama-2-SFT compared to Llama-2 i.e., the Llama-2-SFT representations diverge from those of control models which specialize in individual tasks. This means that training on multiple tasks encourages the model to learn more general representations in the lower layers. The authors call these layers as shared layers, because their representations are shared across tasks.
• In the middle layers (10-15), there is a signficant transition, with Llama-2-SFT model exhibiting high similarity to all control models. Since control models specialize in individual tasks, a high similarity means that these layers encode a high degree of task-specific information. The authors call these layers as transitional layers, as the transition to task-specific representations coccurs within these layers.
• This trend continues, albeit to a lesser extent, up to final layers (16-32), which the authors call refinement layers. In these layers, the model continues to refine its representations towards task-specific predictions.

Examining individual task clusters

As Figure-3 demonstrates, for tasks that are not well encoded in the pre-trained Llama-2 (structured data to text generation, translation), the CKA similarities for Llama-2-SFT remained high throughout layers 10-32 (transition and refinement layers). Instruction Tuning resulted in significant representational shifts, especially for these tasks.

Do the representational effects of instruction tuning generalize to unseen tasks?

To analyze how well the findings generalize to unseen tasks, the authors held out 7 out of 60 tasks from the FLAN 2021 dataset and instruction-tuned the model on remaining 53 tasks.

• For lower layers (upto 12), Llama-2 model exhibited slightly higher CKA similarities than Llama-2-SFT model for several tasks, indicating that while Llama-2-SFT model was not explicitly trained on these tasks, it produced more divergent representations in lower layers and thus more general than the ones produced by Llama-2.
• However, as we move to middle and higher layers, Llama-2-SFT model began matching and ultimately surpassing the CKA similarities of Llama-2 model.

Also, high variances in CKA similarities across tasks, suggests that we cannot identify transition layers for Llama-2-SFT model in this setup, just shared and refinement layers.

Conclusion

• LMs instruction tuned on multiple tasks learned different representations in lower layers compared to LMs tuned on individual tasks. (Such representations could be shared and used across tasks)
• There are clear differences between pre-trained and instruction-tuned models, with most significant representational transformations occuring in the middle transitional layers. (further highlights the critical role of middle layers in encoding the specialized task knowledge induced by instruction tuning)
• In the refinement layers, instruction-tuned models continue to shape representations toward specific tasks but without substantial representational changes with respect to task-specific information.
• The mapping doesn’t generalize to unseen tasks, revealing that a potential additional reason for the strong generalization capabilities of instruction-tuned models to unseen tasks can be related to their multi-task nature of producing more general representations.

References

Zheng Zhao, Yftah Ziser, and Shay B Cohen. 2024. Layer by Layer: Uncovering Where Multi-Task Learning Happens in Instruction-Tuned Large Language Models. In Proceedings of the 2024 Conference on Empirical Methods in Natural Language Processing, pages 15195–15214, Miami, Florida, USA. Association for Computational Linguistics.